SGP2019 - Graduate School Course
Università degli Studi di Milano
Spectral Geometry Processing
Giuseppe Patanè, CNR-IMATI
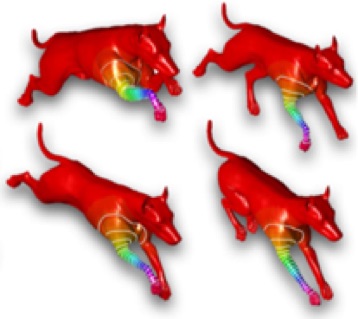
Abstract In geometry processing and shape analysis, several applications have been addressed through the properties of the spectral kernels and distances, such as commute-time, biharmonic, diffusion, and wave kernel distances. Spectral distances are easily defined through a filtering of the Laplacian eigenpairs and have been applied to shape segmentation and comparison with multi-scale and isometry-invariant signatures. In fact, they are intrinsic to the input shape, invariant to isometries, multi-scale, and robust to noise and tessellation.
In this context, this course is intended to provide a background on the properties, discretization, computation, and main applications of the Laplace-Beltrami operator, the associated differential equations (e.g., harmonic equation, Laplacian eigenproblem, diffusion and wave equations), the Laplacian spectral kernels and distances (e.g., commute-time, biharmonic, wave, diffusion distances). While previous work has been focused mainly on specific applications of the aforementioned topics on surface meshes, we propose a general approach that allows us to review the Laplacian kernels and distances on surfaces and volumes, and for any choice of the Laplacian weights.
All the reviewed numerical schemes for the computation of the Laplacian spectral kernels and distances are discussed in terms of robustness, approximation accuracy, and computational cost, thus supporting the audience in the selection of the most appropriate method with respect to shape representation, computational resources, and target applications.
Duration: ~90-105 minutes (6 June 2019, 14:00-15:45)
Course Material & Main References
-
• Presentation [PDF] (last update: 08 July, 2019)
-
• Patanè G., Laplacian Spectral Kernels and Distances: Definition, Computation, and Applications to Geometry Processing and Shape Analysis. Morgan&Claypool Publisher. 2017. DOI: http://dx.doi.org/10.2200/S00781ED1V01Y201705VCP029
-
• Patanè G., A Unified Definition and Computation of Laplacian Spectral Distances, Patter Recognition, Volume 93, September 2019, Pages 68-78. DOI: https://doi.org/10.1016/j.patcog.2019.04.004 [PDF]
-
• Patanè G., Laplacian spectral basis functions, Computer-Aided Geometric Design, 65: 31-47 (2018). DOI: https://doi.org/10.1016/j.cagd.2018.07.002 [PDF]
-
• Patanè G., STAR - Laplacian spectral kernels and distances for geometry processing and shape analysis, STAR-State- of-the-Art Report. In: Computer Graphics Forum, 35(2): 599-624 (2016). DOI: http://dx.doi.org/10.1111/cgf.12866 [PDF]
-
• Patanè G., An introduction to Laplacian spectral kernels and distances: theory, computation, and applications. SIGGRAPH Course, 2017. 30 July-3 August 2017, Los Angeles (USA). DOI: http://dx.doi.org/10.1145/3084873.3084919 [PDF]
Giuseppe Patanè is researcher at CNR-IMATI (2006–today) Institute for Applied Mathematics and Information Technologies—Italian National Research Council, and member of the Shape and Semantics Modelling Group. Since 2001, his research activities have been focused on the definition of paradigms and algorithms for modeling and analyzing digital shapes and multidimensional data. He received a Ph.D. in Mathematics and Applications from the University of Genova (2005) and a Post-Lauream Degree Master in Applications of Mathematics to Industry from the F. Severi National Institute for Advanced Mathematics, Department of Mathematics and Applications—University of Milan (2000). He has authored many scientific publications and book chapters on spectral shape analysis, surface segmentation, parameterization, and approximation with implicit functions. He is author of 2 books, 1 Eurographics STAR, 2 SIGGRAPH ASIA Courses, 1 Eurographics Course, and 1 SMI Course. He has co-chaired SMI2019 and SMI2015, and one ISPRS workshop.
Contact: patane@ge.imati.cnr.it
Home Page: http://pers.ge.imati.cnr.it/patane/Home.html
Acknowledgements
- People
-
•Shape and Semantics Modelling Group, CNR-IMATI, Italy
-
•SGP2019 Conference & Graduate School Chairs: Marcel Campen & Sylvain Lefebvre
- Projects
-
•H2020 ERC-AdG CHANGE
-
•IMAGE-FUSION, Biannual Project funded by Regione Liguria & EU FESR
