3D-from-2D Curve-Skeleton Extraction
Marco Livesu, Fabio Guggeri, Riccardo Scateni
During the first part of my PhD I focused on the problem of computing
curve-skeletons of 3D shapes. This is a well known problem in computer
graphics and many algorithms have been proposed in literature in recent years.
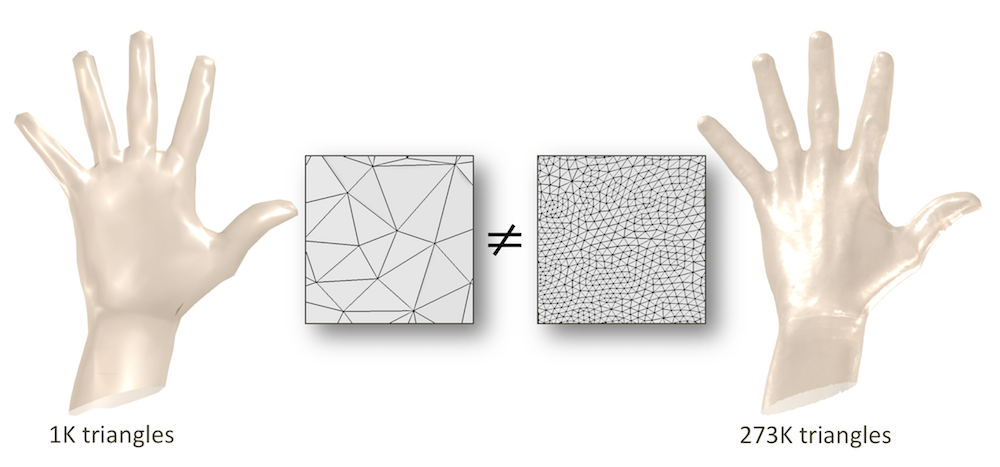
We observed that most of these algorithms are tightly coupled with the discretization of the shape, both in terms of what type of primitives are used to represent its surface (triangles, points, voxels, implicit functions...) and in terms of resolution. Consequently, two objects that the human brain may perceive as almost identical, like the two hands shown in the figure below, are usually seen as two completely different entities by skeletonization algorithms and, thus, may produce very different skeletons
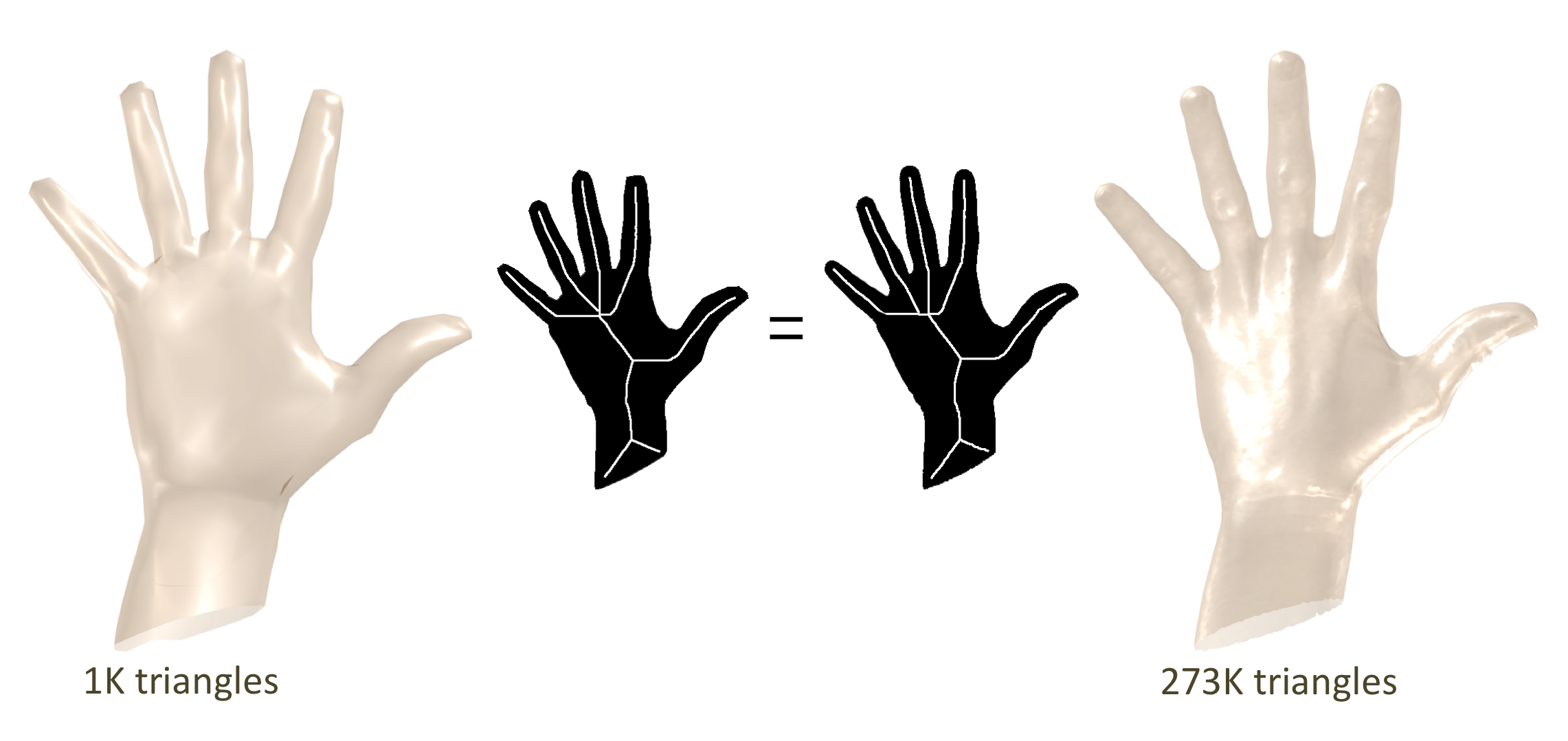
The intuition behind our work is twofold: on the one side we observed that whatever the discretization of a shape is, its visual appearance will be consistent with the object being represented. For example the two hands above will produce very similar silhouettes, if observed from the same point of view
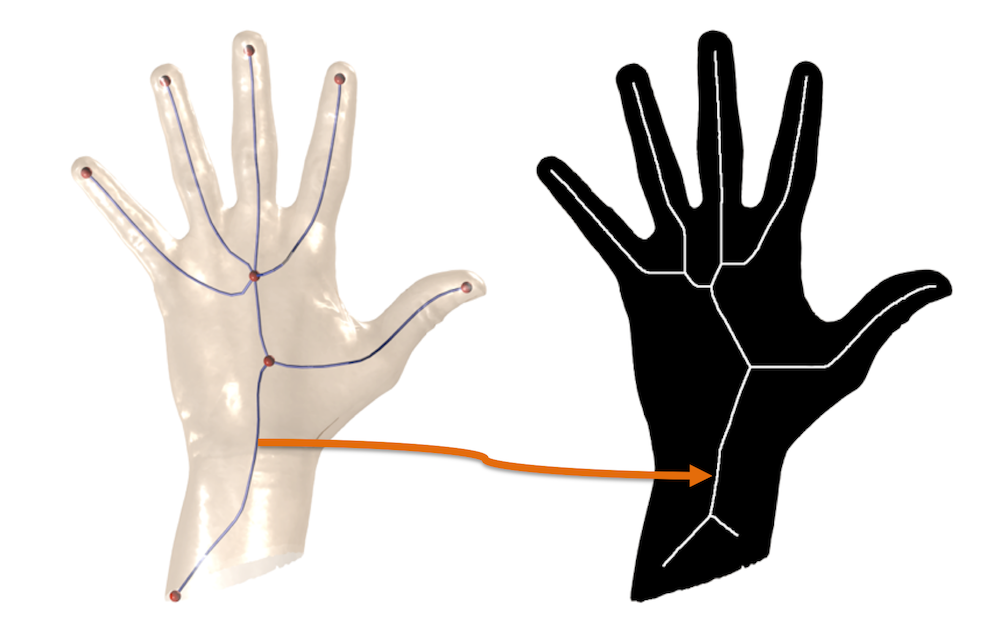
On the other hand, we noticed that in absence of occlusion there is quite an interesting relation between the curve-skeleton of a 3D shape (left) and the medial axis of its silhouette (right). In fact, the curve-skeleton roughly projects over the medial axis!
We therefore implemented a set of algorithms that exploit this relation and are able to extract the curve-skeleton of a 3D shape just by analysing a small number of its silhouettes as observed from different points of view.
The main advantages of this approach are:
Here are some videos that date back to 2010, when I was still a master student and had just started to look into this topic
The results of our research are summarized in three scientific papers and a PhD thesis:
We observed that most of these algorithms are tightly coupled with the discretization of the shape, both in terms of what type of primitives are used to represent its surface (triangles, points, voxels, implicit functions...) and in terms of resolution. Consequently, two objects that the human brain may perceive as almost identical, like the two hands shown in the figure below, are usually seen as two completely different entities by skeletonization algorithms and, thus, may produce very different skeletons

The intuition behind our work is twofold: on the one side we observed that whatever the discretization of a shape is, its visual appearance will be consistent with the object being represented. For example the two hands above will produce very similar silhouettes, if observed from the same point of view

On the other hand, we noticed that in absence of occlusion there is quite an interesting relation between the curve-skeleton of a 3D shape (left) and the medial axis of its silhouette (right). In fact, the curve-skeleton roughly projects over the medial axis!

We therefore implemented a set of algorithms that exploit this relation and are able to extract the curve-skeleton of a 3D shape just by analysing a small number of its silhouettes as observed from different points of view.
The main advantages of this approach are:
- independence from the discretization - we can deal with triangle meshes, quad meshes, polygon meshes, polygon soups, implicit surfaces, voxel-based shapes an more. As long as there exist a way to take a snapshot of a shape and detect its silhouette, we are good
- independence from the resolution - the number of primitives used to describe a shape is meaningless as long as the visual appearance of the shape is preserved
- highly resistent to noise, missing parts, holes, degenerate primitives and so forth - the silhouette space is much more robust than the geometric space in which shapes are embedded. This naturally makes our algorithms extremely robust
Here are some videos that date back to 2010, when I was still a master student and had just started to look into this topic
The results of our research are summarized in three scientific papers and a PhD thesis:
- Reconstructing the Curve-Skeleton of 3D Shapes Using the Visual Hull
Marco Livesu, Fabio Guggeri, Riccardo Scateni
IEEE Transactions on Visualization and Computer Graphics (TVCG, 2012)
[ PDF, PPT, BibTex ] - Practical Medial Axis Filtering for Occlusion-Aware Contours
Marco Livesu, Riccardo Scateni
STAG - Smart Tools and Apps for Graphics 2015 (Verona, Italy)
[ PDF, PPT, BibTex ] - Extracting Curve-Skeletons from Digital Shapes Using Occluding Contours
Marco Livesu, Riccardo Scateni
The Visual Computer (CGI 2013, Hannover, Germany)
[ PDF, PPT, BibTex ] - Understanding The Structure of 3D Shapes:Poycubes and Curve-Skeletons
Marco Livesu
PhD Thesis (University of Cagliari, 2014, Italy)
[ PDF, PPT, BibTex ]
