We consider the problem of relaxing a discrete (n − 1) dimensional hyper surface defining the boundary between two adjacent n dimensional regions in a discrete segmentation. This problem often occurs in computer graphics and vision, where objects are represented by discrete entities such as pixel/voxel grids or polygonal/polyhedral meshes. A common approach consists in assigning to each element of the domain a value (or label). Elements sharing the same label belong to the same region, whereas elements with different labels belong to different regions. 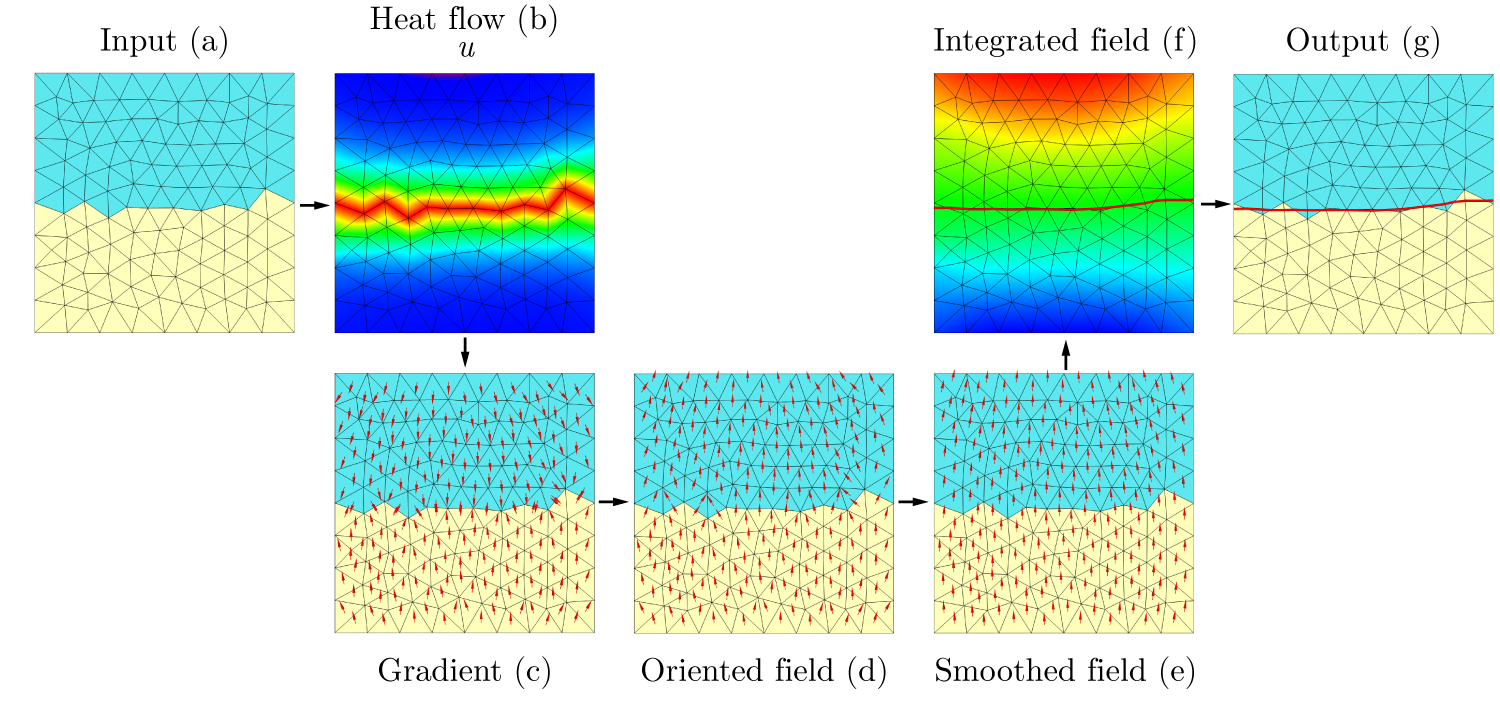Segmentation boundaries are therefore only intrinsically defined, and amount to the union of the interfaces between adjacent elements having different label, which tend to be geometrically poor and expose a typical jagged behavior. We propose a relaxation scheme that replaces the original boundary with a smoother version of it, defined as the level set of a continuous function. 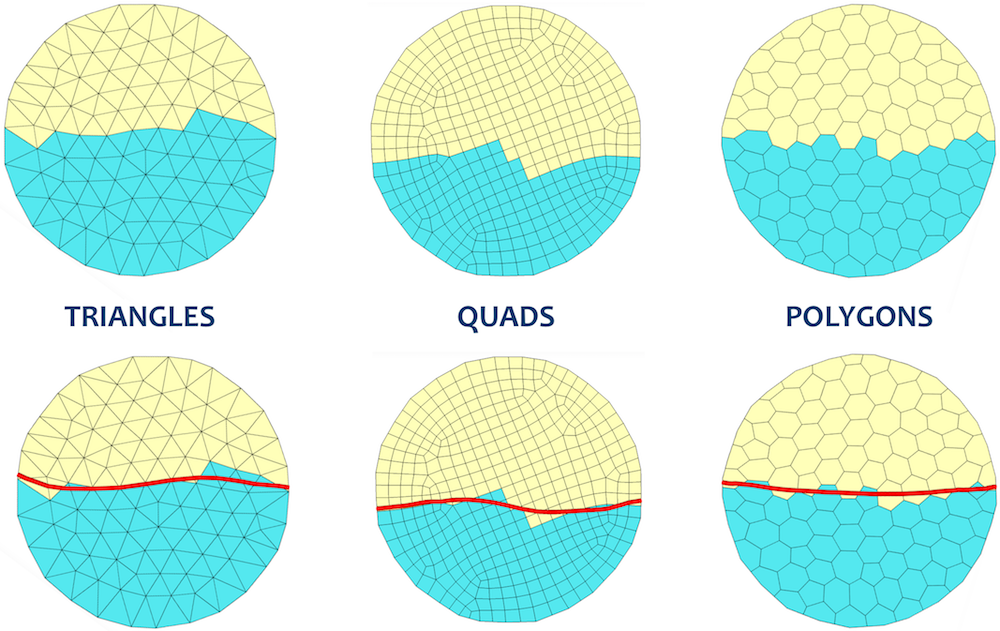The problem has already been considered in recent years, but current methods are specifically designed to relax curves on discrete 2-manifolds embedded in R^3, and do not clearly scale to multiple discrete representations or to higher dimensions. Our biggest contribution is a smoothing operator that is based only on three canonical differential operators: namely the Laplacian, gradient and divergence. These operators are ubiquitous in applied mathematics, are available for a variety of discretization choices, and exist in any dimension. 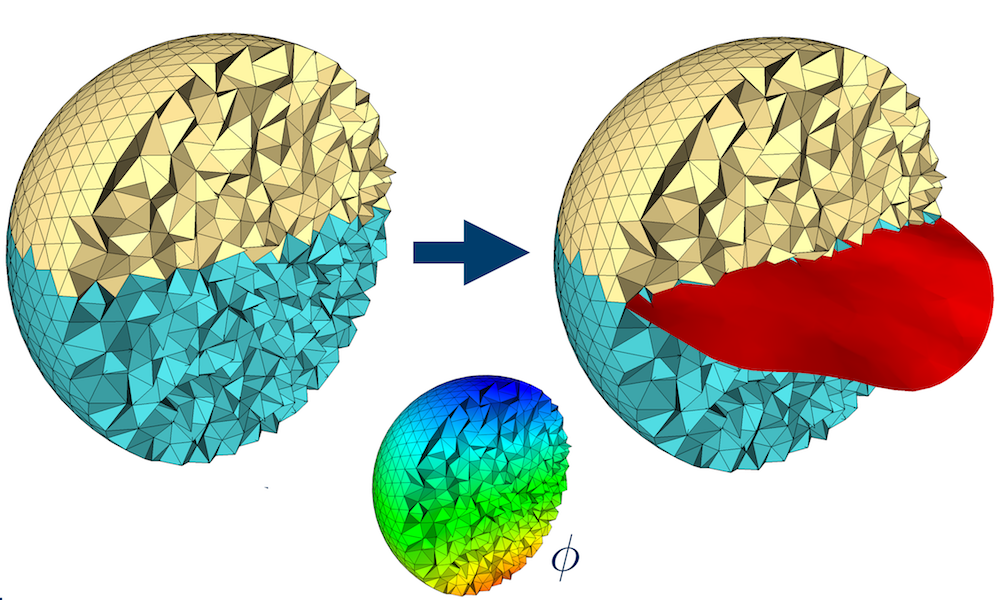To the best of the author’s knowledge, this is the first intrinsically dimension-independent method, and can be used to relax curves on 2-manifolds, surfaces in R^3, or even hyper-surfaces in R^n. As such, not only it is useful to refine the boundaries of discrete segmentations, but also for applications like data mining, where clustering in high dimensional spaces often occur, and the refinement of the clusters’ boundaries may be beneficial for classification algorithms.

          @article{Liv17_extended,
            author    = {Livesu, Marco},
            title     = {A Heat Flow Relaxation Scheme for n Dimensional Discrete Hyper Surfaces},
            journal   = {Computers \& Graphics},
            year      = {2018},
            volume    = {71},
            pages     = {124 - 131},
            issn      = {0097-8493},
            doi       = {10.1016/j.cag.2018.01.004}}

          @inproceedings{Liv17,
            author    = {Livesu, Marco},
            booktitle = {Smart Tools and Apps for Graphics - Eurographics Italian Chapter Conference},
            title     = {{Heat Flow Based Relaxation of n Dimensional Discrete Hyper Surfaces}},
            year      = {2017},
            publisher = {The Eurographics Association},
            ISBN      = {978-3-03868-048-2},
            DOI       = {10.2312/stag.20171222}}